Zenos Paradoxon
Schlappe Logik
»Ein logischer Kurzschluss beim Philosophieren«
Algorithmisch aufgelöst und dargestellt
Das Zitat
„Zeno von Elea (ca. 470 v. Chr.) war einer der frühesten westlichen Philosophen, deren Ideen überliefert sind. Er ist bekannt vor allem wegen seines „Paradoxons der Bewegung. … Zeno wollte mit seinen Beweisen zeigen, dass Bewegung unmöglich sei, und die Vorstellung der Lächerlichkeit preisgeben, dass Raum und Zeit unendlich teilbar seien.
Der berühmteste Beweis stammt von Achilles und einer Schildkröte. Achilles läuft mit der Schildkröte, der er einen Vorsprung gegeben hatte, um die Wette.
Um sie zu überholen, muss er zunächst die Distanz zwischen sich und der Schildkröte laufen, in dieser Zeit aber hat sich die Schildkröte schon wieder ein wenig bewegt, weshalb Achilles diese neue Distanz überbrücken muss etc.
Daraus folgt, dass Achilles niemals die Schildkröte einholen und schon gar nicht überholen kann.
Das Zitat
Dieses Paradoxon hat bislang keine akzeptierte Lösung gefunden und bezeugt die eigentliche Merkwürdigkeit der Vorstellung, dass Raum und Zeit unendlich teilbar seien.“ (1)
Modell und Wirklichkeit
Ich habe den Hasen und den Igel als Wettläufer genommen. Im tatsächlichen Lauf läuft der Hase los und holt den Igel ein - entsprechend dem folgenden einfachen physikalischen Modell, welches einen direkten Bezug zum tatsächlichen Lauf hat.
Die beiden laufen mit den konstanten Geschwindigkeiten vH und vI - der Hase hat den anfänglichen Vorsprung Δ0.
Der Hase holt den Igel zur Zeit T ein:
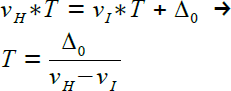
Der oben gezogene logische Schluss „Daraus folgt“ ist nicht zulässig, denn die Aussage (in roter Schrift) ist wahr nur für Zeiten t, die kleiner als T sind (t < T), und der logische Schluss bezieht sich auf Zeiten, die gleich oder größer als die Einholzeit T sind. Ein Widerspruch.
Logik führt also nicht zwangsläufig zu neuen Wahrheiten, sondern kann den Philosophen auch schlicht in die Irre leiten. Hier ist Mathematik gefragt und nicht die naive Anwendung von logischen Sätzen.
Die oben gemachte Aussage hat keinen direkten Bezug zum tatsächlichen Geschehen. Der Ablauf wird hier in unendlich viele Schritte unterteilt. Unendlich viele Schritte? Die kosten doch unendlich viel Zeit - könnte ein Philosoph denken!
Es wird so algorithmisch ein gänzlich artifizieller Ablauf modelliert - ein Bewegungsmodell für den tatsächlichen Bewegungsablauf. Der logische Schluss - gezogen aus diesem Bewegungsmodell, der Hase könne den Igel nicht einholen, ist falsch. Denn das Bewegungsmodell gibt die endliche Einholzeit korrekt wider.
Im folgenden Text soll nun die Einholzeit basierend auf dem Bewegungsmodell berechnet werden.
Die Algorithmisierung
|
Hase |
Igel |
|
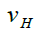
|
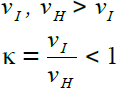
|
Konstante Geschwindigkeit des Hasen und des Igels |
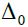
|
Vorsprung des Igels zur Startzeit T0 |
|
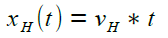
|
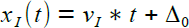
|
Bewegungsgleichungen |
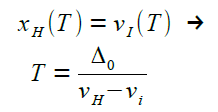
|
Die Einholzeit T ist schnell ausgerechnet! |
|
|
Ich möchte die oben gemachte Aussage nun algorithmisch nachbilden - mit knappen Worten: Zur Zeit Tn+1 ist der Hase an dem Ort, an dem der Igel zur Zeit Tn war. |
||
|
Hase |
Igel |
|
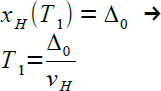
|
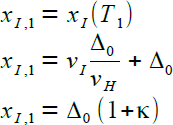
|
Zur T1 ist der Hase am Ort Δ0 und der Igel am Ort xI,1 |
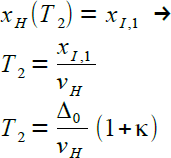
|
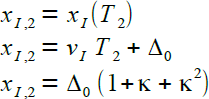
|
Zur T2 ist der Hase am Ort xI,1 und der Igel am Ort xI,2 |
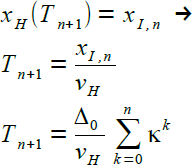
|
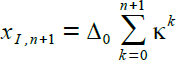
|
Zur Tn+1 ist der Hase am Ort xI,n und der Igel am Ort xI,n+1 |
|
Hase |
Igel |
|
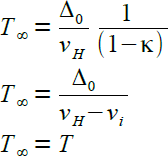
|
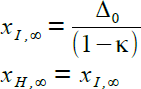
|
Grenzwert n → ∞ Die durch die Reihenbildung erhaltene Einholzeit ist gleich der oben auf direktem Wege berechneten Einholzeit. |
Der Algorithmus hat unendlich viele Schritte, aber der Hase holt den Igel in endlicher Zeit ein.
Die unendlich vielen Rechenschritte sind reine mathematische Abstraktion, die endliche Einholzeit ist praktische Physik.
Der Epilog
"Diese und ähnliche Argumente Zenons setzen voraus,
dass Entfernungen und Geschwindigkeiten
unendlich teilbar sind. ...
Aristoteles, der die Rätsel Zenons überliefert hat,
glaubte sie entkräftet und damit die Möglichkeit
von Bewegung bewiesen zu haben,
indem er zwischen zwei Arten der Unendlichkeit unterschied: der wirklichen
und der potentiellen Unendlichkeit.
Doch es sollte noch viele Jahrhunderte dauern,
bis die von Zenon aufgeworfenen Fragen Lösungen erhielten, die sowohl
die Philosophen als auch die Mathematiker
zufriedenstellten." (2)
Hanebüchener Unsinn
Sage ich!
Leider gibt der Autor keinen weiteren Hinweis auf die
Lösungen, die die Philosophen zufriedenstellten.
Der Epilog
Entfernungen und Geschwindigkeiten sind fehlerbehaftete physikalische Messgrößen, deren Werte üblicherweise mit Fließkommazahlen angegeben werden.
Zu jeder kleinen Zahl gibt es natürlich eine Zahl, die noch kleiner ist, aber das hat mit den Messgrößen und mit Physik rein gar nichts zu tun.
Und irgendwann kommt bei aller Kleinheit auch dem Philosophen die Quantenphysik in die Quere - und dann sieht die Welt wieder ganz anders aus.
Der Epilog
Philosophie -
Worte für bare Münze
Eine großartige Wortschwurbelei durch die Jahrhunderte
Die Referenzen
(1) - Das erste Zitat ist entnommen dem schönen und empfehlenswerten Buche:
David Papineau (Hrsg.)
Philosophie
Eine illustrierte Reise durch das Denken
WBG (Wissenschaftliche Buchgesellschaft)
Darmstadt, 2006
Die Referenzen
(2) - Das zweite Zitat ist entnommen dem insgesamt vierbändigen und ebenfalls empfehlenswerten Werk:
Anthony Kenny
Geschichte der abendländischen Philosophie
Band 1: Antike
WBG (Wissenschaftliche Buchgesellschaft)
Darmstadt, 2012
Beiträge
| Paradoxon | Zeno von Elea, 470 v. Chr. |
| Literatur | Anthony Kenny, David Papineau |
| Webgerüst | impress |
| Foliensatz | Bernd Ragutt |
| Erstellt | Im Sommer 2011 |
| Geändert | Im Frühling 2015 |